FIL I.4 – Active Filters

Introduction

In the previous post we went over passive LC filter design. LC filters do have many advantages: they are simple to understand and design and they don’t require an external power supply. They also are the only solution for higher frequencies. That said, they cannot provide gain. Instead, some power is lost when the signal goes through the filter. This is a filter’s insertion loss. For extremely weak signals, this can be quite problematic. The higher the order of the LC circuit, the bigger the insertion loss.

This is where active filters come in. Since they can provide gain, they shine in their ability to filter very weak signals. They can also manage higher power levels. On the experimental side of things, they also do not need inductors, which makes construction faster and cheaper. Not to mention no inductors means no parasitic coupling of unwanted frequencies. They do have their drawbacks though, and the most critical one is the bandwidth of the active device. Active filters usually cannot be used above certain frequencies.

Active Filter Design

Active filter design greatly benefits from software design tools, even more so than for passive LC ladder filters. There are more parameters to take into account for an active filter, and the math behind is a bit more involved.

That said, there are still many similarities between passive and active filter design. Active filters can still be designed for a specific kind of response: they all belong to one of the filter families described in earlier posts:

the Butterworth famiily, offering a flat passband response and shallow rolloff
the Chebyschev family, offering a much steeper rolloff at the cost of ripple in the passband
the Bessel family, offering a flat passband response, good group delay characteristic, and very shallow rolloff
the Cauer family, offering the steepest rolloff at the cost of ripple in the passband, and notches in the stopband

Just like passive filters, active filter rolloff after the cut-off frequency (also called corner frequency) is 20dB/decade power wise per order, or 10dB/decade voltage wise per order.

Where active filter design differs the most is the amount of available topologies to choose from. For passive filters, LC ladders, whether “T” or “Pi” configurations, were all that was needed. Active filters, on the other hand, can have very different characteristics not only based on their filter family, but also on which active filter topology is used.

Due to the relatively large number and the complexity of these topologies, in this post we’re only going to cover the two most common filter topologies: the Sallen-Key topology, and the Multiple Feedback (MFB) topology.

Sallen-Key Active Filters

The Sallen-Key filter, also called Sallen-and-Key filter, or VCVS (Voltage Controlled Voltage Source) filter, is the most popular and common active filter topology. And for good reason, while it may not offer the most performance, it is the easiest to understand and design, and still gives more than adequate responses. Here are the Sallen-Key architectures for low-pass, high-pass, and band-pass filters:

Notice that for the low-pass and high-pass filters, we have two capacitors. This gives the configuration a second-order response. The band-pass filter is a special case: just like for passive filters, even if it has 4 capacitors, it still gives a second-order response.

To understand how this filter works, let’s study the low-pass variant. A low frequencies, the capacitor is an open circuit: so the input signal goes directly to the Op-Amp, with a certain gain. The input signal is replicated (with gain if there is some) at the output. A high frequencies, the capacitors are shorts. At the input of our op-amp, the signal is sent to ground by the low impedance of the capacitor, hence almost no voltage is being amplified. A these higher frequencies, notice that this circuit not only has negative feedback with the resistor divider network, but also positive feedback with $C_1$ . Varying this capacitor can change the peak response of our filter at cut-off frequency. Making it larger decreases impedance at cut-off frequency, thus increasing positive feedback and increasing the peak response. Making it smaller has the opposite effect.

However, the same reason $C_1$ provides positive feedback also gives the Sallen-Key filter its main disadvantage. At higher frequencies, above the cut-off point, $C_1$ acts like a short. This means a portion of our signal is no longer being filtered, but instead directly coupled to our output. This means that above a certain frequency in the stop-band, attenuation decreases.

Also, notice how the output is non-inverting: the input signal is applied the non-inverting input of the op-amp.

The two $RC$ networks define the cut-off frequency, while $R_3$ and $R_4$ determine the gain of the filter. Notice how $R_3$ and $R_4$ are arranged in a non-inverting amplifier configuration, giving a gain of $K= 1 + \frac{R_4}{R_3}$ . The cut-off frequency is $f_c = \frac{1}{2\pi\sqrt{R_1 R_2 C_1 C_2}}$ , which is very similar to the $RC$ first-order filter. Finally, the Q-factor of this filter is $Q=\frac{\sqrt{R_1 C_1 R_2 C_2}}{R_1 C_2 + R_2 C_2 + R_1 C_1 (1-K)}$

Higher order filters can be created by chaining multiple of these configurations together. This will always result in an even-ordered filter. Odd-ordered active filters using the Sallen-Key configuration can be created by inserting a simple single-order RC active filter before the remaining stages. Unfortunately, when chaining multiple stages together to achieve a higher order filter, the component values will often not be identical from one stage to the next. So how we do start designing a Sallen-Key active filter?

Let’s start be defining our design constraints. For this example, let’s say we want:

a 4th order Butterworth low-pass filter
a cut-off frequency of 10kHz.

The first step is to define a few ratios that will simplify our equations and help us to better visualize a solution:

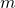$m = \frac{R_1}[R_2}$ : $m$ is the resistor ratio
$n = \frac{C_1}{C_2}$ : $n$ is the capacitor ratio

Next, we need to look up design tables for Sallen-Key Butterworth filters. A good design handbook will have them. If you’re not too keen on spending 100 dollars for one, the data is available on TI’s wonderful app note here, on page 9.

In these tables, we have two parameters for each stage: FSF, and Q. FSF is the frequency scaling factor, and Q is the quality factor. After having chosen your filter order, and thus the number of stages your Sallen-Key configuration will have, use the following equations, also available on page 9 of TI’s app note, to find the actual component values. For each stage:

$K = 1 + \frac{R_4}{R_3}$ : the gain of the stage

*** QuickLaTeX cannot compile formula:
FSF \times f_c = \frac{1}{2\pi\sqrt{R_1 R_2 C_1 C_2}

*** Error message:
File ended while scanning use of \frac .
Emergency stop.

, with 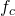$f_c$ being our chosen cut-off frequency

$Q = \frac{R_1 R_2 C_1 C_2}{R_1 C_2 + R_2 C_2 + R_1 C_2 (1-K)}$

You’ll notice only that with just FSF and Q given in the tables, this still gives us quite a lot of choice for determining our resistances and capacitors. A common simplification used when designing Sallen-Key filters is to let both the resistor ratio and the capacitor ratio be unity. This means $R_1=R_2= R$ , and $C_1=C_2=C$ . The above equations then become:

$FSF f_c = \frac{1}{2\piRC}$
$Q = \frac{1}{3 - K}$

These equations are much more manageable! There are downsides to using this simplification however. The quality factor $Q$ now depends on K, and we can’t have a negative Q or null Q, so our gain $K$ needs to be less than 3. When designing Sallen-Key filters, another very common simplification is to let gain $K$ be unity. Thus our filter becomes:

The unity gain Sallen-Key filter is a very common design. With $K=1$ , all resistances equal, and all capacitances equal, our Q-factor becomes $\frac{1}{2}$ .

A quick reminder on filter Q: Q is a filter’s peakness at its pole frequency, here our cut-off frequency. A this frequency, gain will be Q. For a 1V input signal, a Q factor of 2 will give us an amplitude of 2V at the cut-off frequency. The higher the Q, the higher the response peaks at cut-off frequency.

The Unity-Gain Sallen-Key Filter

Now, while all these simplifications do make it easier to manually calculate the component values, they don’t give the greatest filter performance. Keeping the popular unity-gain design, but foregoing the equal resistances and equal capacitances assumption, we have two equations:

$FSF f_c = \frac{1}{2\pi\sqrt{R_1 R_2 C_1 C_2}}$
$Q = \frac{R_1 R_2 C_1 C_2}{R_1 C_2 + R_2 C_2}$

for 4 parameters: $R_1$ , $R_2$ , $C_1$ , $C_2$ . Instead of setting $R_1=R_2$ , and $C_1=C_2$ , we can instead optimize the ratios depending on what we’re trying to achieve.

An important consideration is whether we should go for higher resistances and lower capacitances, or lower resistances but higher capacitances. This depends on your filter’s operating environment. If the stage preceding the filter has a rather high output impedance, it makes sense to go for higher resistance values, so as to avoid loading the previous stage too much. On the other hand, if you’re going to operate the filter at high frequencies, it might be better to go for higher capacitance values so as to swamp out the parasitic capacitances present in the circuit.

Not forcing equal resistances and capacitances also allows us to have different Q-values for different stages. Combining different stages with different Q-values allows for better response curves overall.

Here is the response curve for a unity-gain Sallen-Key low-pass filter with a cut-off frequency of 10kHz:

Notice how attenuation stops at around 100kHz, and the signal is amplified again. This is a drawback to the Sallen-Key configuration.

You might wonder what is the point of a unity gain active filter. Isn’t the whole point of an active filter to provide gain in addition to filtering? Do keep in mind that while this filter has no gain, it has no attenuation either, something that plagues passive filters. Active filters also generally have steeper rolloff near the cut-off frequency.

Adding Gain or Attenuation to the Sallen-Key Filter

While the unity-gain variant of the Sallen-Key filter is very popular, sometimes you still want some gain or attenuation.

Attenuation is the simplest to add. A simple voltage divider before $R_2$ allows us to attenuate the input signal level:

The voltage a point A then becomes $\frac{R_a}{R_a + R_b} \times V_{in}$ . To obtain the exact same circuit response, we also need to ensure that the output resistance of this voltage divider stays equal to $R_1$ . This way, the active filter “sees” the same thing, and the response is unchanged. This means:

$R_1 = R_a // R_b$

This filter now has an attenuation of $\frac{R_a}{R_a + R_b}$ .

Adding gain isn’t that much more complicated. We simply add in a voltage divider network in the negative feedback loop to provide non-inverting gain:

as was shown in the initial presentation of the Sallen-Key configuration. Note however, that adding gain like this will change the circuit’s Q-factor, and thus component values. While attenuation can be added after filter design, gain has to be included in the initial filter design and not added afterwords. The Q-factor becomes:

$Q = \frac{R_1 R_2 C_1 C_2}{R_1 C_2 + R_2 C_2 + R_1 C_2 (1-K)}$

as was shown earlier.

The Multiple Feedback Filter

The next most popular active filter is the Multiple Feedback Filter (MFB), also called the infinite-gain multiple feedback filter. Here are the architectures for low-pass, high-pass, and band-pass variants:

To understand how this filter works, let’s look at the low-pass variant in more detail. Notice that at low frequencies, when the capacitors act as open-circuits, the filter acts like an inverting amplifier. $R_1$ and $R_2$ set the filter’s gain. At higher frequencies, most of the signal is shorted to ground by the low impedance of $C_1$ .

Note here that if we want to create a unity gain MFB filter, we need to set $R_1$ and $R_2$ equal. However, practical component tolerances means that our gain will always be slightly off. A Sallen-Key filter does a better job at keeping a true unity gain since its unity gain doesn’t depend on external components. Also note that for unity gain designs, the Sallen-Key filter requires 1 less component than the Multiple Feedback Filter: 4 instead of 5.

The MFB filter also gets rid of the previous filter’s stopband problem: here the signal is continually attenuated throughout the frequency range.

Also, the MFB filter is inverting. The input signal is applied at the inverting input of the op-amp.

Which One Should I Choose?

Now that we’ve covered the two most popular active filter configurations out there, the obvious question is, which one should you use? It all depends on your application and what filter response you want.

As a general rule, Sallen-Key filters are more sensitive to variations in component values. Thus, for higher gain and Q-factors, your measured response can actually vary from your calculations by a wide margin. Thus, for higher Q and gain applications, MFB is the way to go.

When making low-pass filters, either design will give you adequate performance in the passband and near the cut-off frequency, with a slight advantage going to the Sallen-Key configuration (it is less noisy). However, keep in mind that the attenuation in the stopband isn’t constant in the case of the Sallen-Key filter. At one point in the stopband, attenuation will stop, and even reverse, as seen in the above graphs. If you don’t care about this fact, then go for the Sallen-Key configuration.

When making high-pass filters, the Sallen-Key configuration is generally preferred. Look at the high-pass variant of the MFB filter. Notice the two capacitors paving the way from input to output. At higher frequencies, these two capacitors acts as a low impedance path to the output. This results in spikes in the passband response. The Sallen-Key configuration doesn’t suffer from this drawback.

When making bandpass filters, which one you go for depends on your filter’s eventual gain and Q-factor. Usually, bandpass filters have higher Q-factor requirements. Due to the sensibility of the Sallen-Key factor to component value, the Multiple Feedback filter is usually preferred in this scenario.

There are plenty of other active filter configurations to choose from. But these two will probably satisfy most, if not all, of your demands.

Active Filter Stage Order

We’ve said previously that multiple active filters could be cascaded to increase filter order and improve the response. Does it matter in which order we organize these stages? In theory, you should obtain the exact same response no matter how you organize your stages. However, there are real-world practical reasons for why you would order stages in a certain way. Nearly all filter handbooks, tables, and filter software will pre-order your stages based on Q-factor or gain: from lowest to highest. If we had the highest Q stages first, then these op-amps would need a greater voltage range (remember, Q-factor determines voltage gain at cutoff frequency) to follow the input. On the other hand, if we put low Q-factor and low gain filters first, the voltage range of the op-amps wouldn’t have to be extended. By the time the signal arrives at the higher Q and higher gain stages, it would have been sufficiently attenuated by the previous lower Q stages that the output wouldn’t be dramatically high, thus requiring less voltage range from the op-amp.

There is a reason why you would want to put higher Q and higher gain stages first however: that is if you are aiming for low-noise operation. A large enough gain for the first stage will make the noise impact of successive stages insignificant. An in-depth treatment of noise is in the works and will be published soon.

A Word on Gain

We saws that it was possible to design active filters with gain. While this seems useful, and it is, we need to be cautious as to when and how we add gain. The biggest limitation of active filters is their active device’s (most often an op-amp) bandwidth. When designed for unity gain, an op-amp’s bandwidth is relatively high, in the MHz range. However, when gain is added that bandwidth decreases (for an in-depth explanation as to why this happens, check out this post on negative feedback and bandwidth). Give too much gain and your response will plummet as your op-amp can’t keep up. It is often times a better idea to design for unity-gain, and then add gain as an extra stage after the filter, thereby separating filtering stages and gain stages.

Practical Design of Active Filters

You’ll notice that I haven’t given you a step by step explanation as to how to calculate the component values of each filter. While it made sense to do so for passive LC ladder filters for educational purposes, doing the same for active filters would be very tedious, considering the increased complexity of each design. Instead, I wanted to give you an intuitive understanding of the two types of filters and show you their architecture. Of course, i won’t leave you without giving you a way to actually design your active filters.

The best tool I’ve come across so far for active filter design is Analog Devices’ Filter Wizard Tool. It’s an easy to use online tool for designing both Sallen-Key and Multiple Feedback filters. It’s also where I got all the response curves for this post. The interface is sweet and intuitive. If you need some guidance, Analog Devices has a few videos on how to use it. Just by watching this one you should be good to go.

When to Use Active Filters

A few simple questions is all you need to determine if you should use a passive or active filter for your design:

if you’re designing a high frequency filter, anything above a few MHz, use a passive filter. Op-amp bandwidth is just too small for these applications.
if you’re filtering high amounts of power, go for passive filters.
when you just want something small and simple: use passive filters.
when you want to drive something (speakers for example), or want a low output resistance, try using an active filter. Passive filters usually need to be buffered or impedance matched.
for audio applications, active filters typically excel.

Conclusion

That was a long post! Hopefully this post was helpful as a good introduction to active filters. Of course, you don’t need to learn the architectures by heart. It is a good idea however to know when active filters shine, and where their limits are. In ham circuits, active filters are most often seen in the audio stages of a receiver or transmitter, while RF and IF filters are passive.

We’ve covered the two most popular active filters here, but there is a wealth of information on plenty of other types of active filters available on the internet and in good textbooks. If you’re curious to know more but don’t know where to start, go check out state-variable filters and switched-capacitor filters.