AMP I.12 – The Common Gate Amplifier

Introduction

The last of the JFET classical amplifier configuration is the common gate amplifier, analogous to the common base BJT amplifier. As usual, we will derive the voltage gain, current gain, input resistance, and output resistance of this configuration.

The Common Gate Amplifier

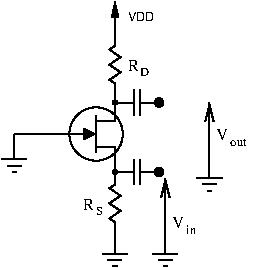
For the common gate amplifier, the input signal is applied at the source, while the output signal is sampled at the drain. As you can see, the gate itself is grounded: the gate is “common”.

Voltage Gain

To derive the voltage gain, let’s draw the small signal equivalent circuit:

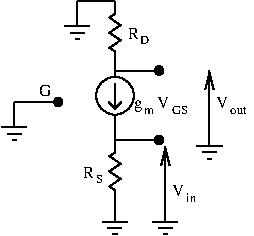
As usual, let’s express $v_{out}$ and $v_{in}$ to find the voltage gain $A_v$ :

$v_{out} = V_{DD} - R_D I_D = V_{DD} - R_D g_m v_{GS}$
$v_{GS} = v_G - v_S = -v_S = -v_{IN}$ , with $v_G =0$ because the gate is grounded

Substituting $v_{GS}$ in the first equation gives:

$v_{out} = V_{CC} + R_D g_m v_{in}$

We can now calculate our voltage gain:

$A_v = \frac{\Delta v_{out}}{\Delta v_{in}} = R_D g_m$

If we add a load, this gain becomes $A_v = (R_D // R_L) g_m$

Current Gain

To find the current gain, we need to add a load, and determine the input and output current.

Let’s express $i_{in}$ . A node equation at the source terminal gives us:

$i_{in} = g_m v_{GS} - \frac{v_{in}}{R_S}$

Since $v_{GS} = v_G - v_S = -v_S = -v_{in}$ (gate is grounded), we have:

$i_{in} = -g_m v_{in} - \frac{v_{in}}{R_S} = -v_{in}(g_m + \frac{1}{R_S})$

Let’s express $i_{out}$ next, using ohm’s law. We already know the output voltage $v_{out}$ since it was calculated in the previous section.

$i_{out} = \frac{v_{out}}{R_L} = \frac{g_m R_D // R_L v_{in}}{R_L}$

We can now derive the current gain $A_i$ :

$A_i = \frac{i_{out}}{i_{in}} = \frac{g_m R_D // R_L}{R_L} \times \frac{1}{g_m + \frac{1}{R_S}}$

$A_i = \frac{g_m R_D // R_L}{R_M} \times \frac{R_S}{g_m R_S +1}$

By approximating $g_m R_S +1 \approx g_m R_S$ , we obtain:

$A_i = \frac{g_m R_D // R_L \ times R_S}{R_L g_m R_S} = \frac{R_D // R_L}{R_L}$

As we can see, $A_i < 1$ . Our current gain is less than unity. For $R_L$ relatively low compared to $R_D$ , we have $A_i \approx 1$ . This is why you will often see people say the common gate amplifier has unity current gain.

Input Resistance

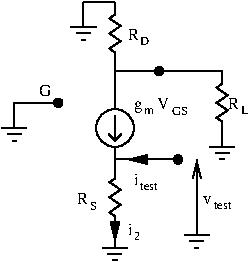
To find the input resistance, we apply a test signal at the input and calculate $R_{in} = \frac{v_{test}}{i_{test}}$ :

$g_m v_{GS} = -g_m v_S = -g_m v_{test}$
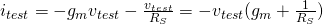$i_{test} = -g_m v_{test} - \frac{v_{test}}{R_S} = -v_{test}(g_m + \frac{1}{R_S})$ , node equation at the source terminal

This gives us: $R_{in} = \frac{1}{g_m + \frac{1}{R_S}} = \frac{R_S}{R_S g_m +1} \approx \frac{1}{g_m}$ .

The input resistance of the common gate amplifier is low.

Output resistance

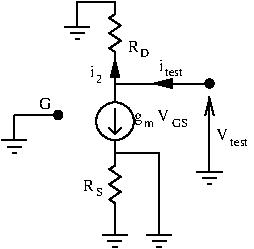
To find our output resistance, we remove the load and ground the input. Then, we apply a test signal at the output and calculate $R_{out} =\frac{v_{test}}{i_{test}}$ .