Introduction
No component is as connected to ham radio history than the quartz crystal. Still today, thanks to their excellent frequency stability and cost-effectiveness, crystal oscillators in one form or another dominate the electronic landscape. You’ll find them in nearly every electronic device you can think of, from PC motherboards to your wristwatch. And, of course, radio receivers. While they may be very old technology, dating back to the early 19th century, contrary to the LC oscillator it has withstood the test of time. Short of the most demanding applications, crystal oscillators are a cheap and extremely precise option.
A Brief Introduction to Crystals
Before diving into crystal oscillators, we should first explain how crystals actually work. What we call a crystal is a thinly sliced section of quartz. Quartz itself isn’t an electrical component, but the reason crystals can be used in electronic circuits is because of its piezoelectric effect. When mechanically stressed or distorted, a small voltage is created. Likewise, when excited by a certain voltage, the quartz crystal vibrates, or resonates. However, they can’t do so at any voltages. Depending on how the quartz is sliced and how thick it is, it will have a lower or higher resonance frequency. A thicker slice will resonate at a lower frequency than a thinner slice. The first frequency that a quartz can resonate at is its fundamental resonance frequency. Technically, a quartz crystal can also resonate at any multiple of the fundamental resonance frequency. In practice however, crystal manufacturers cut the crystals in such a way as to prioritize either the fundamental frequency, or one of its multiples, also called its overtones.
One of the reasons why crystals are so popular are their extremely high Q factor: compared to traditional LC resonant circuits, the changes in impedance when approaching resonant frequency is extremely abrupt. This makes crystal oscillators extremely stable, but also greatly limits their tuning range if we want a variable oscillator.
To better understand and exploit crystals, we make use of a crystal’s equivalent circuit:
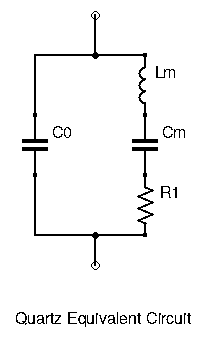
It looks very similar to an LC resonant circuit! In the series branch, 
is called motional capacitance, while 
is the motional inductance. Together they define the crystal’s series resonance frequency. The parallel capacitance 
, along with both and define the crystal’s parallel resonance frequency. Already we see that this component has two different resonance frequencies. In series resonance, impedance is lowest ( and cancel out, leaving the very small 
), while at parallel resonance impedance is highest.
Since the parallel resonant circuit consists of and the series equivalent capacitance of and (which is lower than alone), the parallel resonance frequency is higher than the series resonance frequency (remember 
). The series resonance will appear as a notch in the crystal’s impedance graph, and happens at a lower frequency than the parallel resonance, indicated by a spike in impedance magnitude.
Since crystals can have two different resonant frequencies, manufacturers specify which resonant frequency their crystal was built for. Hence, both series-resonant and parallel-resonant crystals exist. For our purposes, we will nearly always use series-resonant crystals.
Making a Crystal Oscillator
As seen above, crystals are basically very high Q LC tank circuits, which make them perfect for creating stable and accurate oscillators. The fact that crystals inherently “contain” an LC circuit inside means we don’t need to include one in our oscillator circuit, saving space, time, and cost. Crafting an oscillator with a crystal follows the same principles as designing an LC oscillator. If you compare LC oscillators and quartz oscillator circuits, you will find many similarities. Just like with LC oscillators, you can often identify a Colpitts or Hartley configuration. The example below illustrates a series-tuned Colpitts crystal oscillator:
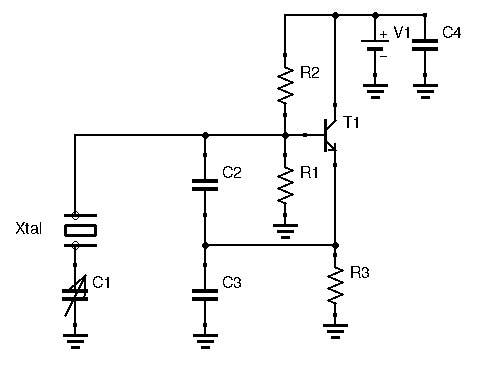
Notice there is a trimmer capacitor in series with the crystal. Quartz are specified for a certain load capacitance. Indeed, manufacturers don’t know what the crystal will be connected to, and extra capacitances in the circuit will contribute to a different resonance frequency. To actually get the frequency the crystal was built for, matching the load capacitance to the recommended value in the datasheet gives better results. In many cases, not matching the capacitances will still give a working oscillator, albeit sometimes with a different frequency than expected. In many designs, such as the one given above, you will see a trimmer capacitor in series with the crystal to adjust the load capacitance. After some circuit testing, its value can then be chosen based on the frequency we want.
This trimmer can also serve as a tuning capacitor. While the crystal has a certain operating frequency that its manufacturer suggests, it will still resonate at frequencies that are close enough to it. This is often called “pulling the crystal”. This phenomenon makes the creation of VXOs – Variable Crystal Oscillators – possible. These are much more accurate and stable than their LC counterparts. However, they have extremely limited tuning range. For a wider range of frequency tuning, multiple quartz crystals are needed.
Just like for LC oscillators, you don’t exactly design a crystal oscillator from scratch. Instead, you start from an existing circuit, adjusting values and tweaking it to your liking. Many circuits you will find can be adapted for a large range of HF frequencies. More than probably any kind of circuit you will encounter, crystal oscillators require some tweaking and adjusting to get the response you actually want. Make sure you use the prescribed kind of crystal the designer suggests. If no information is available, you should probably go for a series-resonant crystal.
You’ll notice I’m not giving you many crystal oscillator or VXO circuit examples. This is because, with the components and technology available today, I don’t believe incorporating a hand-made crystal oscillator in your designs in the best path. Building a working crystal oscillator can be a fun and educational experience. However, to go through all the effort of designing one to, in the end, just be able to tune to maybe one quarter of an HF band will probably be very frustrating to many. This may have been a great introduction to amateur radio’s more technical side a few decades ago, but newcomers to the hobby will probably not be impressed.
Using Crystal Oscillators in your Designs
While I don’t think VXO are a great option for your receiver if you want versatility, there is one thing a crystal oscillator is absolutely great for: acting as a super stable reference frequency. This reference frequency can then be used in either analog or digital frequency synthesis, a topic we will get into very shortly. Both these methods offer a very wide tuning range, and with a crystal oscillator acting as their reference frequency, their outputs can be very stable as well.
While you could use a crystal oscillator design and build it yourself with a regular quartz crystal, I believe the best solution is to simply buy a prepackaged crystal oscillator set to the reference frequency you wish to use. Ordered online, bare crystals will cost anywhere from a few cents to over a dollar each. These crystals will need to be incorporated inside an oscillator circuit, such as the one shown above, to be of any use. Prepackaged crystal oscillators, on the other hand, offer the whole thing: crystal and the necessary circuitry to make it into an oscillator, in one small-sized package. These often come in 4-lead packages. You simply need to hook up a power supply and a ground, and you’ve got a stable sine-wave at the output pin. These prepackaged oscillators can also come in temperature-compensated, or even oven-controlled variants for even greater stability. Best of all, they barely cost more than a bare crystal, rarely going for over 2 or 3 dollars apiece.
Conclusion
While traditional LC oscillators or variable crystal oscillators were some of the most iconic circuits of the ham literature, it is difficult to recommend newcomers to incorporate them in their designs. The archaic components they use are difficult to find and expensive, and their tuning range will probably frustrate many hams. Instead, we should embrace the advances we’ve had in the field of radio technology, and look towards frequency synthesis for our variable oscillators. Crystals still have a fundamental role to play here, acting as stable references.